处理数据时用到了小提琴图，看了四分位点的计算公式，但是和numpy的percentile()函数对应不上，记录一下具体的计算方式。

小提琴图

一般来说，小提琴图是一种绘制连续型数据的方法，可以认为是箱形图与核密度图的结合体。在小提琴图中，我们可以获取与箱形图中相同的信息。

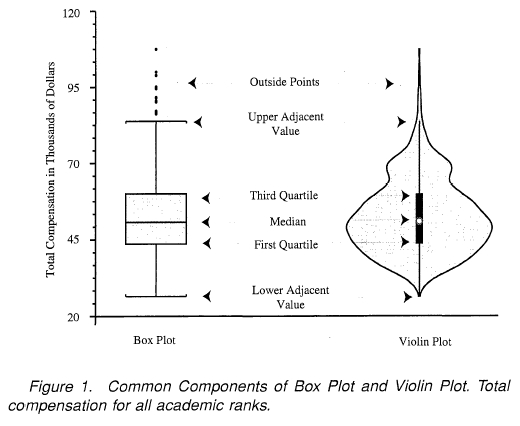
  • 中位数（小提琴图中的一个白点）
  • 四分位数距(Inter Quartile Range, IQR)：小提琴图中心的黑色粗条
  • Upper adjacent value：Third Quartile + 1.5 * IQR
  • Lower adjacent value：First Quartile - 1.5 * IQR
  • Upper/lower adjacent value（黑色细线）用来检测离群值，即位于这俩“栅栏“之外的值可被视为离群值。

离群值是一个统计学里的专业术语。在对同一样本进行多次重复测定时，经常会发现在一组测定数据中有某一个或数个测定值看似比其他测定值明显地偏小或偏大。称这种显著偏离的数据为离群值。有疑问的观察值可能是测试中随机波动的极度表现，但还处于统计控制 的范围之内，是属于同一总体的误差，不算离群值。

四分位数

定义

四分位数（Quartile）应用于统计学中的箱线图绘制，是统计学中分位数的一种，即把所有数值由小到大排列并分为四等份，处于三个分割点位置的数值就是四分位数。

如何理解四分位

中位数把数集分成两个50%，下四分位就是把前50%分成两个25%，上四分位就是把后50%，分成两个25%。

如何计算

假设数列一共有n个数。

（1）当(n+1)/4可以整除时，Q1在(n+1)/4位、Q2在(n+1)/2位、Q3在(n+1)·3/4位。

以数列[1 2 2 5 6 9 9]举例：

Q1在第(7+1)/4=2位，即Q1=2

Q2在第(7+1)/2=4位，即Q2=5

Q3在第(7+1)·3/4=6位，即Q3=9

（2）当(n+1)/4不能整除时

以数列[1 2 3 4 5 6 7 8]举例：

Q1在(8+1)/4=2.25位，介于第二和第三位之间，但是更靠近第二位。所以第二位数权重占75%(小数位)，第三位数权重占25%。Q1=(2*0.75+3*0.25)/(0.75+0.25)=2.25

Q2在(8+1)/2=4.5位，即第4和第5位的平均数，Q2=4.5

同理Q3在(8+1)/4*3=6.75位，在第六位和第七位之间，更靠近第7位。所以第7位权重75%，第6位权重25%。Q3=(7*0.75+6*0.25)/(0.75+0.25)=6.75

numpy的percentile()函数

上边计算中所用的方法是n+1的方法。而numpy的percentile()函数使用的是n-1的方法，即：

Q1的位置=1+(n-1)x0.25

Q2的位置=1+(n-1)x0.5

Q3的位置=1+(n-1)x0.75

靠近分位位置的那一个值占较大比重，为位置小数点后的那部分（或者壹减去小数点后的部分，与上边计算方式相似）。例如数列[1 2 3]：Q1=1.5、Q2=2、Q3=2.5；数列[1 2 3 4 5 6 7 8 9]的60%分位点位置=1+(9-1)x0.6=5.8，Q=6x0.8+5x0.2=5.8。测试代码如下：

1
2
3
4
5
6
7
8
import numpy as np
arr = [1, 2, 3]
print(np.percentile(arr, 25))

# 或者
# import pandas as pd
# arr = pd.Series([1, 2, 3])
# print(arr.describe())

参考文献

如何通俗的理解小提琴图

如何计算四分位数值&应用

四分位数

python numpy库np.percentile用法说明